AMC 8 Daily Practice Round 9
Complete problem set with solutions and individual problem pages
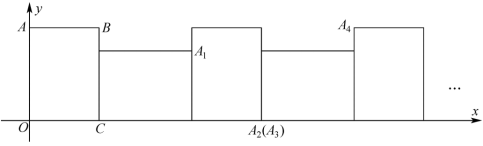
As shown in the figure, a rectangle with length and width rolls continuously along the positive -axis for times. The point sequentially lands at positions . What are the coordinates of ?
- A.
- B.
- C.
- D.
- E.
From the given conditions, we obtain the following sequence of coordinates for point :
Since every four rolls form a cycle, we analyze the displacement per cycle. Each full cycle results in a horizontal shift of:
Thus, after one full cycle, point moves units to the right.
The additional positions within a cycle are as follows:
- After one extra roll, moves units further, and the -coordinate is .
- After two extra rolls, moves units further, and the -coordinate is .
- After three extra rolls, the coordinates are the same as after two extra rolls.
Since:
Point completes full cycles and moves one extra step beyond that.
Thus, the final coordinates are:
The answer is .
