2022 AMC 10 A
Complete problem set with solutions and individual problem pages
Problem 18 Easy
Let be the transformation of the coordinate plane that first rotates the plane degrees counterclockwise around the origin and then reflects the plane across the -axis. What is the least positive integer such that performing the sequence of transformations returns the point back to itself?
- A.
- B.
- C.
- D.
- E.
Answer:A
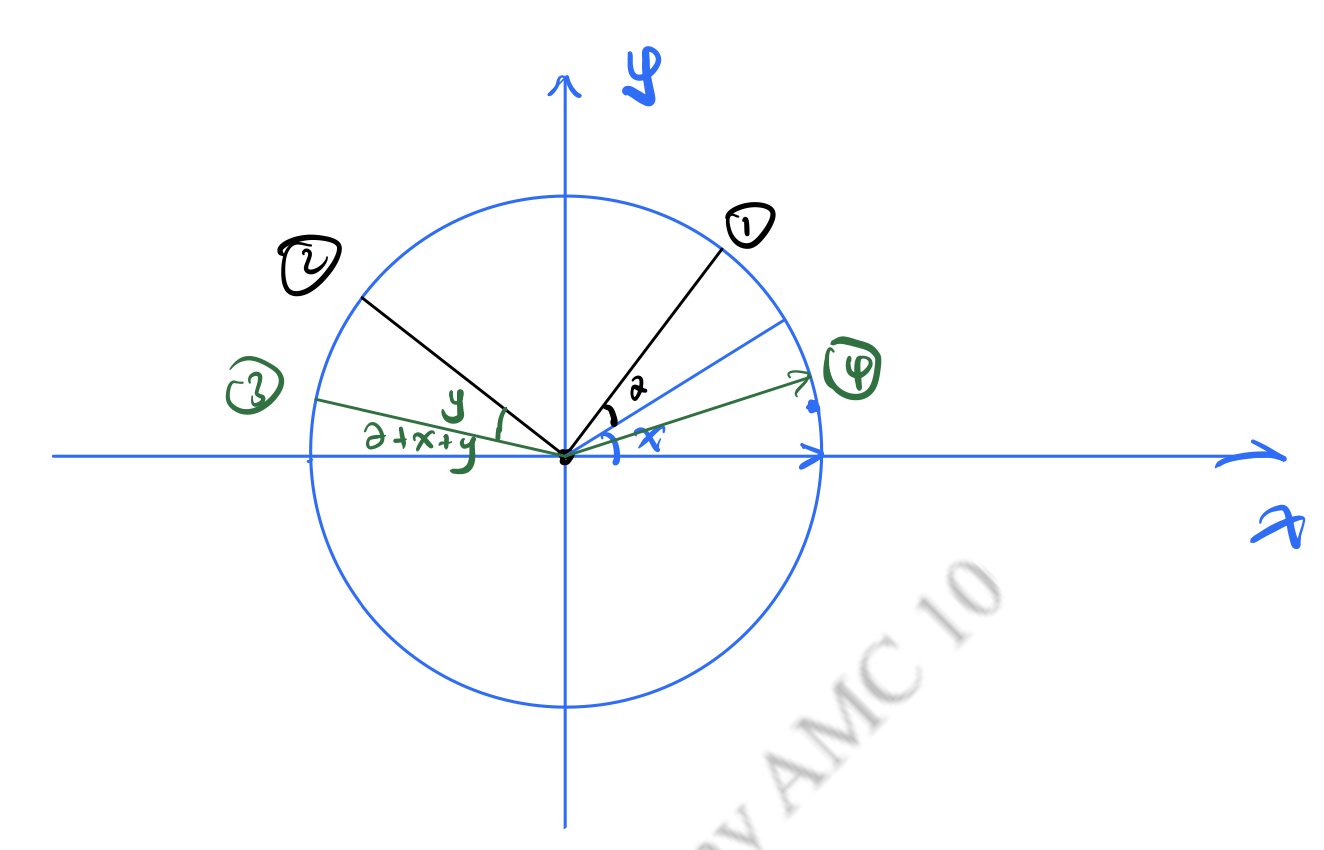
Let the angle between 'the point', 'the origin' and the positive -axis be .
Initially: after .
When , the angle:
.
Back to the original position: , .
When , the angle:
When , .
