2019 AMC 10 B
Complete problem set with solutions and individual problem pages
As shown in the figure, line segment trisected by points and so that .Three semicircles of radius , , and , have their diameters on , and are tangent to line at , , and , respectively. A circle of radius has its center on . The area of the region inside the circle but outside the three semicircles, shaded in the figure, can be expressed in the form , where , , , and are positive integers and and are relatively prime. What is ? (2019 AMC 10B Problem, Question#20)
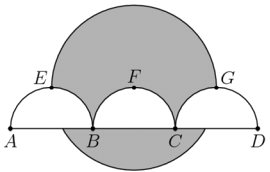
- A.
- B.
- C.
- D.
- E.
Divide the circle into four parts: the top semicircle ; the bottom sector , whose arc angle is because the large circle's radius is and the short length(the radius of the smaller semicircles) is , giving a triangle; the triangle formed by the radii of and the chord , and the four parts which are the corners of a circle inscribed in a square , Then the area is (in , we find the area of the shaded region above the semicircles but below the diameter, and in we find the area of the bottom shaded region).
The area of is ,
The area of is .
For the area of , the radius of , and the distance of (the smaller semicicles' radius ) to .
creates two triangles, so s area is .
The area of is ,
Hence, finding . the desired area is , so the answer is .
