2020 AMC 8
Complete problem set with solutions and individual problem pages
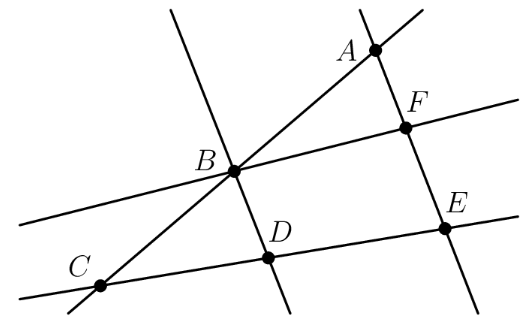
Each of the points and in the figure below represents a different digit from to Each of the five lines shown passes through some of these points. The digits along each line are added to produce five sums, one for each line. The total of the five sums is What is the digit represented by
- A.
- B.
- C.
- D.
- E.
Solution 1
We can form the following expressions for the sum along each line:
Adding these together, we must have , i.e. . Since are unique integers between and , we obtain (where the order doesn't matter as addition is commutative), so our equation simplifies to . This means .
Solution 2
Following the first few steps of Solution 1, we have . Because an even number subtracted from an odd number (47) is always odd, we know that is odd, showing that is odd. Now we know that is 1, 3, or 5. If we try , we get , which is false. Testing , we get , which is also false. Therefore, we have .
