2021 AMC 10 A Fall
Complete problem set with solutions and individual problem pages
How many ordered pairs of real numbers satisfy the following system of equations?
- A.
- B.
- C.
- D.
- E.
Solution 1:
The second equation is . We know that the graph of is a very simple diamond shape, so let's see if we can reduce this equation to that form: We now have two separate graphs for this equation and one graph for the first equation, so let's put it on the coordinate plane: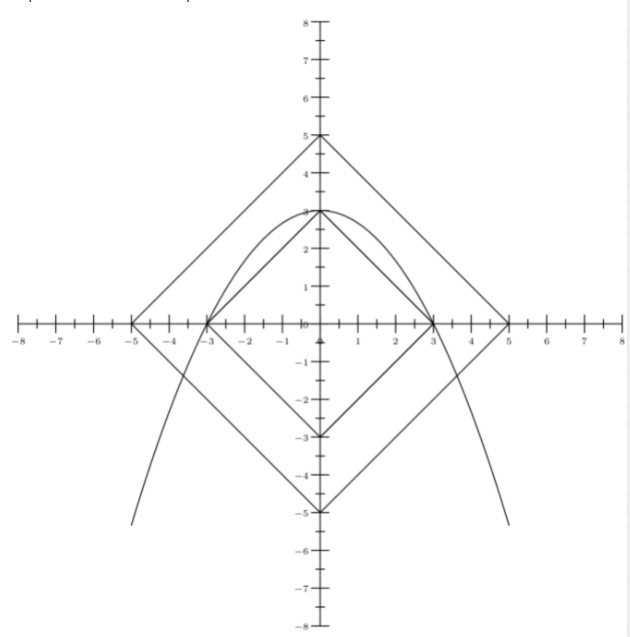
Solution 2:
We can manipulate the first equation to get . From the second equation, we have that or . We will consider each case separately. If , then . The graph of this is a square with vertices , and . The parabola from the first equation is downwards facing, and its vertex is inside this square; the parabola will clearly intersect the square twice. Therefore, this case gives us solutions. If , then . The graph of this is a square with vertices and . The vertex of the parabola from the first equation is on one of the corners of this square (in particular, ). Also, at , the parabola has intercepts of ; the square passes through both of those points. If we continue to move down, the square narrows in, while the parabola continues to expand. Therefore, these are our only 3 intersection points in this case: and . This case gives us solutions. Adding these two cases together, we get our final answer of (D) 5 .
