2020 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 12 Medium

Triangle A M C is isoceles with A M=A C. Medians \overline{M V} and \overline{C U} are perpendicular to each other, and M V=C U=12. What is the area of \triangle A M C ?

  • A.

    48

  • B.

    72

  • C.

    96

  • D.

    144

  • E.

    192

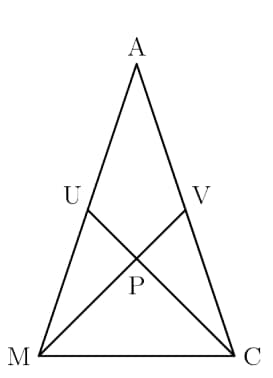
Answer:C

Solution 1:

Since quadrilateral U V C M has perpendicular diagonals, its area can be found as half of the product of the length of the diagonals. Also note that \triangle A U V has \frac{1}{4} the area of triangle \triangle A M C by similarity, so [U V C M]=\frac{3}{4} \cdot[A M C].\quad \frac{1}{4} \cdot 12 \cdot 12=\frac{3}{4} \cdot[A M C].

72=\frac{3}{4} \cdot[A M C] = 96 \rightarrow(\mathbf{C})

Solution 2:

Connect the line segment U V and it's easy to see quadrilateral U V M C has an area of the product of its diagonals divided by 2 which is 72 . Now, solving for triangle AUV could be an option, but the drawing shows the area of A U V will be less than the quadrilateral meaning the the area of A M C is less than 72 * 2 but greater than 72 , leaving only one possible answer choice,C.

Related Problems
Problem 10 2020 AMC 10 A
Problem 11 2020 AMC 10 A
Problem 13 2020 AMC 10 A
Problem 14 2020 AMC 10 A
Think Academy Powered by ChatGPT