2014 AMC 8
Complete problem set with solutions and individual problem pages
Problem 20 Hard
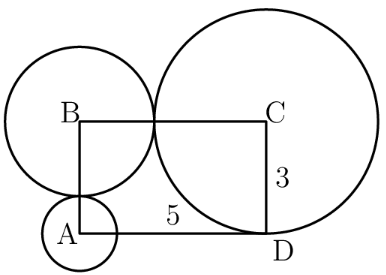
Rectangle has sides and . A circle of radius is centered at , a circle of radius is centered at , and a circle of radius is centered at . Which of the following is closest to the area of the region inside the rectangle but outside all three circles?
- A.
- B.
- C.
- D.
- E.
Answer:B
The area in the rectangle but outside the circles is the area of the rectangle minus the area of all three of the quarter circles in the rectangle.
The area of the rectangle is . The area of all 3 quarter circles is . Therefore the area in the rectangle but outside the circles is . is approximately and substituting that in will give
