2021 AMC 10 A Fall
Complete problem set with solutions and individual problem pages
How many ordered pairs of positive integers exist where both and do not have distinct, real solutions?(2021 AMC Fall 10A, Question #20)
- A.
- B.
- C.
- D.
- E.
Solution 1:
A quadratic equation does not have real solutions if and only if the discriminant is nonpositive. We conclude that: 1. Since does not have real solutions, we have . 2. Since does not have real solutions, we have . Squaring the first inequality, we get . Multiplying the second inequality by 16 , we get . Combining these results, we get We apply casework to the value of : - If , then , from which . - If , then , from which . - If , then , from which . - If , then , from which . Together, there are ordered pairs , namely , and .
Solution 2:
Similar to Solution 1 , use the discriminant to get and . These can be rearranged to and . Now, we can roughly graph these two inequalities, letting one of them be the axis and the other be . The graph of solutions should be above the parabola and under its inverse, meaning we want points on the graph or in the first area enclosed by the two graphs:
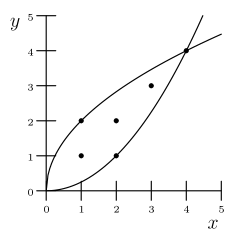
We are looking for lattice points (since and are positive integers), of which we can count (B) 6 .
