AMC 8 Daily Practice - Triangle Properties

Complete problem set with solutions and individual problem pages

Problem 5 Easy

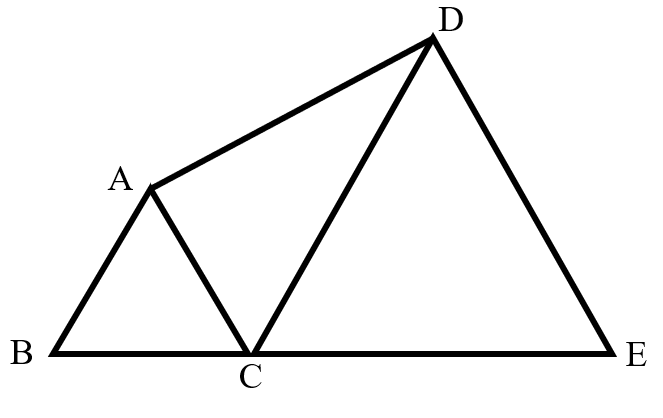
Two equilateral triangles ABC and DCE lie on the same horizontal plane, with areas 4 and 9 respectively. What is the area of triangle ACD?

  • A.

    5

  • B.

    6

  • C.

    6.5

  • D.

    7

  • E.

    8

Answer:B

Since triangles ABC and DCE are equilateral, AB \parallel DC and AC \parallel DE.

Given that the area of a triangle is \frac{1}{2} \times \text{base} \times \text{height}, we have:

\text{Area of } \triangle ABC : \text{Area of } \triangle ACD=AB : DC

\text{Area of } \triangle ACD : \text{Area of } \triangle CDE=BC : DE

Since AB = BC and DC = DE , it follows that: \text{Area of } \triangle ABC : \text{Area of } \triangle ACD = \text{Area of } \triangle ACD : \text{Area of } \triangle CDE.

Let the area of \triangle ACD be A.

Then: A^2 = \text{Area of } \triangle ABC \times \text{Area of } \triangle CDE = 4 \times 9.

Solving for A: A = \sqrt{4 \times 9} = 6.

Thus, the area of \triangle ACD is 6.

Related Problems
Problem 3 AMC 8 Daily Practice - Triangle Properties
Problem 4 AMC 8 Daily Practice - Triangle Properties
Problem 6 AMC 8 Daily Practice - Triangle Properties
Problem 7 AMC 8 Daily Practice - Triangle Properties
Think Academy Powered by ChatGPT