2020 AMC 10 A
Complete problem set with solutions and individual problem pages
As shown in the figure below, a regular dodecahedron (the polyhedron consisting of congruent regular pentagonal faces) floats in empty space with two horizontal faces. Note that there is a ring of five slanted faces adjacent to the top face, and a ring of five slanted faces adjacent to the bottom face. How many ways are there to move from the top face to the bottom face via a sequence of adjacent faces so that each face is visited at most once and moves are not permitted from the bottom ring to the top ring?
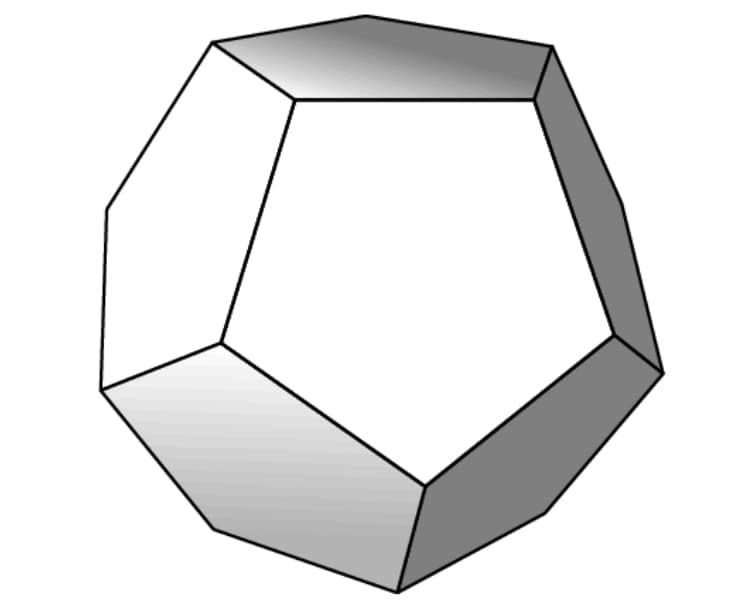
- A.
- B.
- C.
- D.
- E.
Solution 1: Since we start at the top face and end at the bottom face without moving from the lower ring to the upper ring or revisiting a face, our journey must consist of the top face, a series of faces in the upper ring, a series of faces in the lower ring, and the bottom face, in that order.
We have choices for which face we visit first on the top ring. From there, we have choices for how far around the top ring we go before moving down: , or 4 faces around clockwise, , or 4 faces around counterclockwise, or immediately going down to the lower ring without visiting any other faces in the upper ring. We then have choices for which lower ring face to visit first (since every upperring face is adjacent to exactly lower-ring faces) and then once again 9 choices for how to travel around the lower ring. We then proceed to the bottom face, completing the trip. Multiplying together all the numbers of choices we have, we
Solution 2:
Swap the faces as vertices and the vertices as faces. Then, this problem is the same as 2016 AIME I #3which had an answer (E) 810 .
