2025 AMC 8
Complete problem set with solutions and individual problem pages
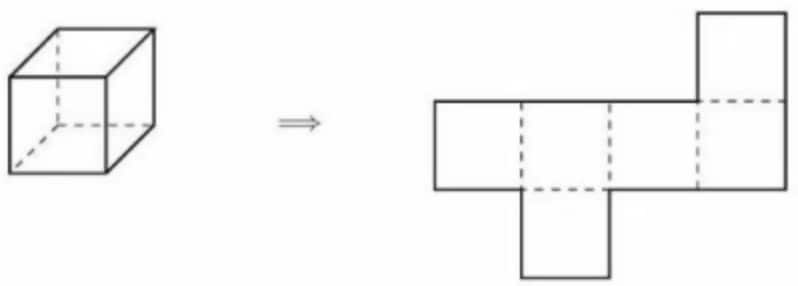
Isaiah cuts open a cardboard cube along some of its edges to form the flat shape shown on the right, which has an area of square centimeters. What is the volume of the cube in cubic centimeters?
- A.
- B.
- C.
- D.
- E.
Solution 1
Each of the faces of the cube have equal area, so the area of each face is equal to , making the side length . From this, we can see that the volume of the cube is
Solution 2
Let the side length of the cube shown be equal to centimeters. The surface area of this cube is equal to the area of the net of the cube, which is equal to square centimeters. The surface area of this cube is also square centimeters, so we have
However, we aren't done. We have found that the side length of the cube is , but the question asks for the volume of the cube, which is equal to cubic centimeters.
