2024 AMC 8
Complete problem set with solutions and individual problem pages
Rodrigo has a very large sheet of graph paper. First he draws a line segment connecting point to point and colors the cells whose interiors intersect the segment, as shown below. Next Rodrigo draws a line segment connecting point to point . How many cells will he color this time?
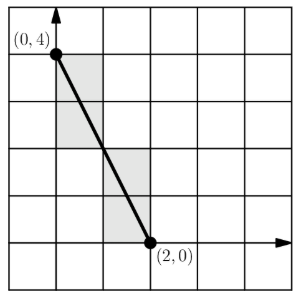
- A.
- B.
- C.
- D.
- E.
Let be the number of cells the line segment from to passes through. The problem is then equivalent to finding
Sometimes the segment passes through lattice points in between the endpoints, which happens times. This partitions the segment into congruent pieces that each pass through cells, which means the answer is
Note that a new square is entered when the lines pass through one of the lines in the coordinate grid, which for happens times. Because and are relatively prime, no lattice point except for the endpoints intersects the line segment from to This means that including the first cell closest to The segment passes through cells. Thus, the answer is Alternatively, can be found by drawing an accurate diagram, leaving you with the same answer.
