2021 AMC 10 A Fall
Complete problem set with solutions and individual problem pages
Isosceles triangle has , and a circle with radius is tangent to line at and to line at . What is the area of the circle that passes through vertices , and (2021 AMC Fall 10A, Question #15)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let be the circle with radius that is tangent to at and to at . Note that . Since the opposite angles of quadrilateral are supplementary, quadrilateral is cyclic. Let be the circumcircle of quadrilateral . It follows that is also the circumcircle of , as shown below:
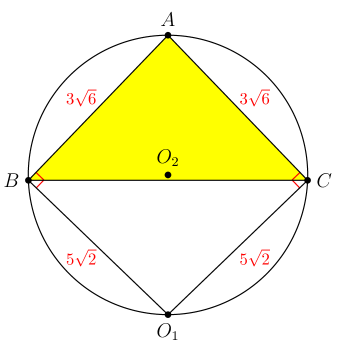
By the Inscribed Angle Theorem, we conclude that is the diameter of . By the Pythagorean Theorem on right , we have Therefore, the area of is .
Solution 2:
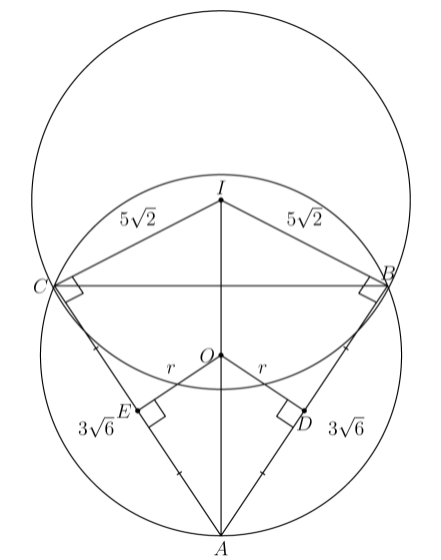
Because circle is tangent to at . Because is the circumcenter of is the perpendicular bisector of , and , so therefore by AA similarity. Then we have . We also know that because of the perpendicular bisector, so the hypotenuse of is This is the radius of the circumcircle of , so the area of this circle is .
