2018 AMC 8
Complete problem set with solutions and individual problem pages
Abby, Bridget, and four of their classmates will be seated in two rows of three for a group picture, as shown.
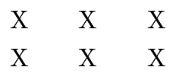
If the seating positions are assigned randomly, what is the probability that Abby and Bridget are adjacent to each other in the same row or the same column?
- A.
- B.
- C.
- D.
- E.
Solution 1
There are a total of ways to arrange the kids.
Abby and Bridget can sit in 3 ways if they are adjacent in the same column:
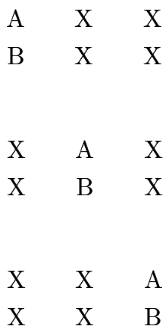
For each of these seat positions, Abby and Bridget can switch seats, and the other 4 people can be arranged in ways which results in a total of ways to arrange them.
By the same logic, there are 4 ways for Abby and Bridget to be placed if they are adjacent in the same row: they can swap seats, and the other people can be arranged in ways for a total of ways to arrange them.
We sum the 2 possibilities up to get or .
Solution 2
We can ignore other students, and treat Abby and Bridget as indistinguishable (since we only care about adjacency, not their order). Thus, the total number of ways is . In one row, they can be adjacent 2 ways: . In one column, they can only be adjacent 1 way: . Add these cases , and therefore, P(Abby and Bridget sitting adjacent) is .
