2015 AMC 8

Solution 1

Let:

- be the number of students who voted in favor of the first issue,

- be the number of students who voted in favor of the second issue,

- be the number of students who voted in favor of both issues.

We are given:

-

-

- students voted against both issues, so the number of students who voted for at least one issue is:

By the principle of inclusion and exclusion:

Substitute known values:

Solution 2

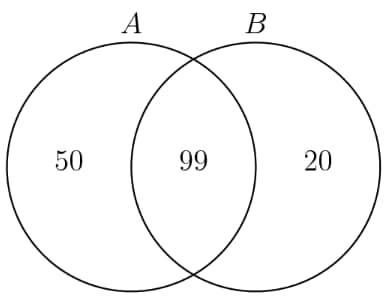
We can see that this is a Venn Diagram Problem.

First, we analyze the information given. There are students. Let's use A as the first issue and B as the second issue.

students were for A, and students were for B. There were also students against both A and B.

Solving this without a Venn Diagram, we subtract away from the total, . Out of the remaining , we have people for A and

people for B. We add this up to get . Since that is more than what we need, we subtract from to get

.