2014 AMC 8

Complete problem set with solutions and individual problem pages

Problem 9 Easy

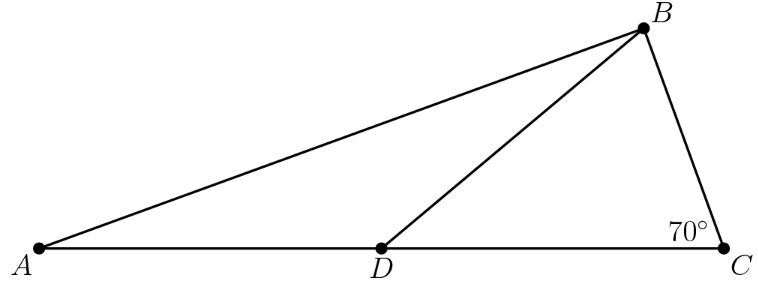
In \bigtriangleup ABC, D is a point on side \overline{AC} such that BD=DC and \angle BCD measures 70^\circ. What is the degree measure of \angle ADB?

  • A.

    100

  • B.

    120

  • C.

    135

  • D.

    140

  • E.

    150

Answer:D

Using angle chasing is a good way to solve this problem. BD = DC, so \angle DBC = \angle DCB = 70, because it is an isosceles triangle. Then \angle CDB = 180-(70+70) = 40. Since \angle ADB and \angle BDC are supplementary, \angle ADB = 180 - 40 = \boxed{\textbf{(D)}~140}.

Related Problems
Problem 7 2014 AMC 8
Problem 8 2014 AMC 8
Problem 10 2014 AMC 8
Problem 11 2014 AMC 8
Think Academy Powered by ChatGPT