2025 AMC 8

Complete problem set with solutions and individual problem pages

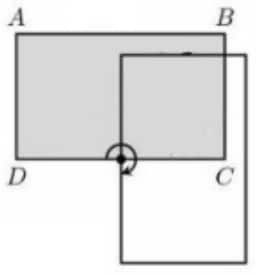
Problem 10 Easy

In the figure below, ABCD is a rectangle with sides of length AB = 5 inches and AD = 3 inches. Rectangle ABCD is rotated 90^\circ clockwise around the midpoint of side DC to give a second rectangle. What is the total area, in square inches, covered by the two overlapping rectangles?

  • A.

    21

  • B.

    22.25

  • C.

    23

  • D.

    23.75

  • E.

    25

Answer:D

The area of each rectangle is 5 \cdot 3 = 15. Then the sum of the areas of the two regions is the sum of the areas of the two rectangles, minus the area of their overlap. To find the area of the overlap, we note that the region of overlap is a square, each of whose sides have length 2.5 (as they are formed by the midpoint of one of the long sides and a vertex). Then the answer is 15+15-2.5^2=\boxed{\textbf{(D)}~23.75}.

Related Problems
Problem 8 2025 AMC 8
Problem 9 2025 AMC 8
Problem 11 2025 AMC 8
Problem 12 2025 AMC 8
Think Academy Powered by ChatGPT