2015 AMC 8

Complete problem set with solutions and individual problem pages

Problem 2 Easy

Point O is the center of the regular octagon ABCDEFGH, and X is the midpoint of the side \overline{AB}. What fraction of the area of the octagon is shaded?

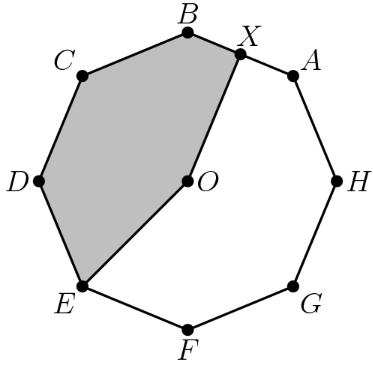
  • A.

    \frac{11}{32}

  • B.

    \frac{3}{8}

  • C.

    \frac{13}{32}

  • D.

    \frac{7}{16}

  • E.

    \frac{15}{32}

Answer:D

Solution 1

Since octagon ABCDEFGH is a regular octagon, it is split into 8 equal parts, such as triangles \bigtriangleup ABO, \bigtriangleup BCO, \bigtriangleup CDO, etc. These parts, since they are all equal, are \frac{1}{8} of the octagon each. The shaded region consists of 3 of these equal parts plus half of another, so the fraction of the octagon that is shaded is \frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{16}=\boxed{\textbf{(D) }\dfrac{7}{16}}.

 

Solution 2

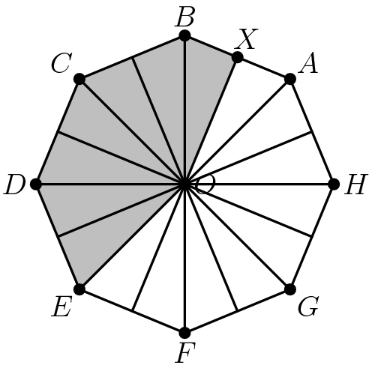
The octagon has been divided up into 16 identical triangles (and thus they each have equal area). Since the shaded region occupies 7 out of the 16 total triangles, the answer is \boxed{\textbf{(D)}~\dfrac{7}{16}}.

Related Problems
Problem 1 2015 AMC 8
Problem 3 2015 AMC 8
Problem 4 2015 AMC 8
Problem 5 2015 AMC 8
Think Academy Powered by ChatGPT