2023 AMC 8
Complete problem set with solutions and individual problem pages
A rectangle, with sides parallel to the -axis and -axis, has opposite vertices located at and . A line is drawn through points and . Another line is drawn through points and . How many points on the rectangle lie on at least one of the two lines?
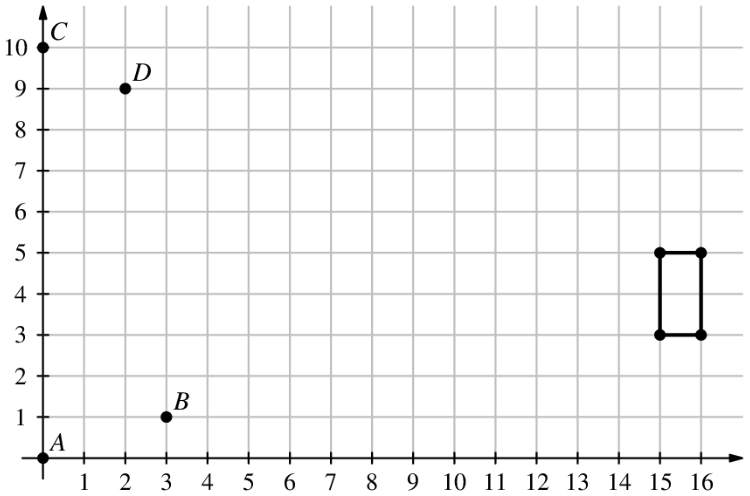
- A.
- B.
- C.
- D.
- E.
Solution 1
If we extend the lines, we have the following diagram:
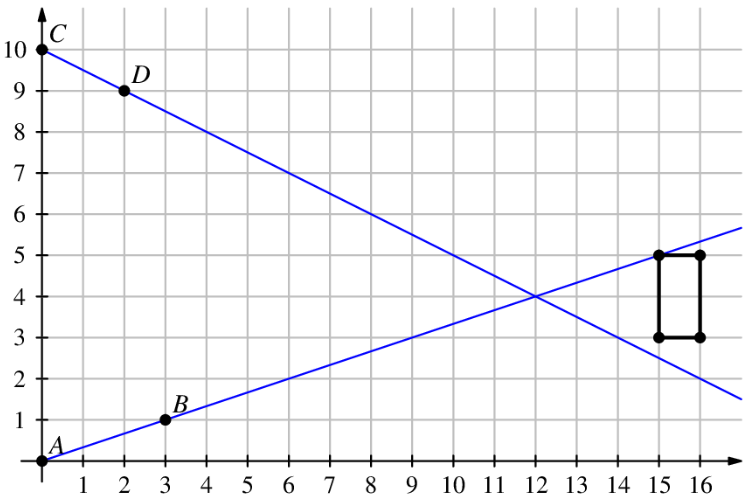
Therefore, we see that the answer is
Solution 2
Note that the -intercepts of line and line are and . If the analytic expression for line is , and the analytic expression for line is , we have equations: and . Solving these equations, we can find out that and . Therefore, we can determine that the expression for line is and the expression for line is . When , the coordinates that line and line pass through are and , and lies perfectly on one vertex of the rectangle while the coordinate of is out of the range (lower than the bottom left corner of the rectangle ). Considering that the value of the line will only decrease, and the value of the line will only increase, there will not be another point on the rectangle that lies on either of the two lines. Thus, we can conclude that the answer is
