AMC 8 Daily Practice - Pythagorean Theorem
Complete problem set with solutions and individual problem pages
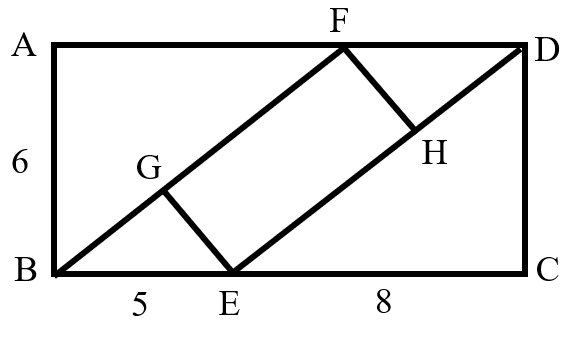
Problem 8 Easy
Quadrilateral is a rectangle. What is the area of the quadrilateral ?
- A.
- B.
- C.
- D.
- E.
Answer:C
Given and , in , we find .
The area of parallelogram can be expressed in two ways:
and .
Thus:
Solving for , we get .
In the right triangle , by the Pythagorean theorem: .
Since , the area of the quadrilateral is: .
Answer: The area of the quadrilateral is square units.
