2018 AMC 8
Complete problem set with solutions and individual problem pages
In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?
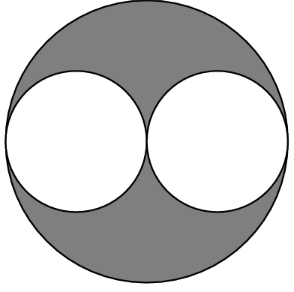
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the radius of the large circle be . Then, the radius of the smaller circles are . The areas of the circles are directly proportional to the square of the radii, so the ratio of the area of the small circle to the large one is ( is of .) This means the combined area of the 2 smaller circles is half of the larger circle, and therefore the shaded region is equal to the combined area of the 2 smaller circles, which is .
Solution 2
Let the radius of the two smaller circles be . It follows that the area of one of the smaller circles is . Thus, the area of the two inner circles combined would evaluate to which is . Since the radius of the bigger circle is two times that of the smaller circles (the diameter), the radius of the larger circle in terms of would be . The area of the larger circle would come to .
Subtracting the area of the smaller circles from that of the larger circle (since that would be the shaded region), we have
Therefore, the area of the shaded region is .
