2019 AMC 8
Complete problem set with solutions and individual problem pages
Problem 24 Hard
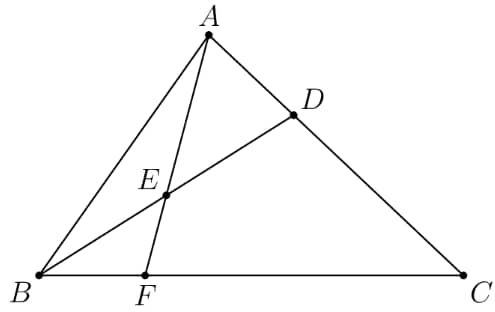
In triangle , point divides side so that . Let be the midpoint of and let be the point of intersection of line and line . Given that the area of is , what is the area of ?
- A.
- B.
- C.
- D.
- E.
Answer:B
Solution 1
We use the line-segment ratios to infer area ratios and height ratios.
Areas:
.
.
Heights:
Let = height (of altitude) from to .
from to is .
from to is .
Conclusion:
, and also .
So, , and thus,
Solution 2
Draw on such that is parallel to .
Triangles and are similar, and since , they are also congruent, and so and .
implies , so , .
Since , , and since , all of these are equal to , and so the altitude of triangle is equal to of the altitude of .
The area of is , so the area of.
