AMC 10 Weekly Practice Round 3

Complete problem set with solutions and individual problem pages

Problem 25 Medium

As shown in the figure, a sphere is inscribed in a cube of side length 2 (the sphere is tangent to each face of the cube). If a point P is chosen at random inside the cube, what is the probability that the point lies outside the sphere?

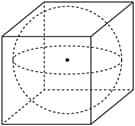
  • A.

    \frac{ \pi }{6}

  • B.

    \frac{ \pi }{8}

  • C.

    \frac{6-\pi }{6}

  • D.

    \frac{8- \pi }{8}

  • E.

    \frac{\pi}{4}

Answer:C

{{V}_{cube}}=2\times 2\times 2=8.

The radius of the inscribed sphere is 1, so its volume is V = \tfrac{4}{3}\pi \times 1^{3} = \tfrac{4}{3}\pi.

The volume of the cube is 2^{3} = 8.

Therefore, the probability that a randomly chosen point in the cube lies outside the sphere is \frac{8 - \tfrac{4}{3}\pi}{8} = \frac{6 - \pi}{6}.

Thus, the answer is \text{C}.

Related Problems
Problem 23 AMC 10 Weekly Practice Round 3
Problem 24 AMC 10 Weekly Practice Round 3
Problem 26 AMC 10 Weekly Practice Round 3
Problem 27 AMC 10 Weekly Practice Round 3
Think Academy Powered by ChatGPT