2023 AMC 8

Complete problem set with solutions and individual problem pages

Problem 24 Hard

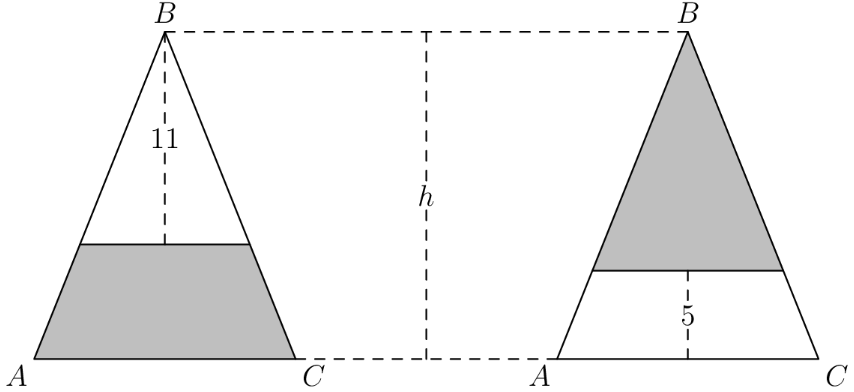
Isosceles \triangle ABC has equal side lengths AB and BC. In the figure below, segments are drawn parallel to \overline{AC} so that the shaded portions of \triangle ABC have the same area. The heights of the two unshaded portions are 11 and 5 units, respectively. What is the height of h of \triangle ABC? (Diagram not drawn to scale.)

  • A.

    14.6

  • B.

    14.8

  • C.

    15

  • D.

    15.2

  • E.

    15.4

Answer:A

Solution 1

First, we notice that the smaller isosceles triangles are similar to the larger isosceles triangles. We can find that the area of the gray area in the first triangle is [ABC]\cdot\left(1-\left(\tfrac{11}{h}\right)^2\right). Similarly, we can find that the area of the gray part in the second triangle is [ABC]\cdot\left(\tfrac{h-5}{h}\right)^2. These areas are equal, so 1-\left(\frac{11}{h}\right)^2=\left(\frac{h-5}{h}\right)^2. Simplifying yields 10h=146 so h=\boxed{\textbf{(A) }14.6}.

 

Solution 2

We can call the length of AC as x. Therefore, the length of the base of the triangle with height 11 is 11/h = a/x. Therefore, the base of the smaller triangle is 11x/h. We find that the area of the trapezoid is (hx)/2 - 11^2x/2h.

Using similar triangles once again, we find that the base of the shaded triangle is (h-5)/h = b/x. Therefore, the area is (h-5)(hx-5x)/2h.

Since the areas are the same, we find that (hx)/2 - 121x/2h = (h-5)(hx-5x)/2h. Multiplying each side by 2h, we get h^2x - 121x = h^2x - 5hx - 5hx + 25x. Therefore, we can subtract 25x + h^2x from both sides, and get -146x = -10hx. Finally, we divide both sides by -x and get 10h = 146. h is \boxed{\textbf{(A)}14.6}.

Related Problems
Problem 21 2023 AMC 8
Problem 22 2023 AMC 8
Problem 23 2023 AMC 8
Problem 25 2023 AMC 8
Think Academy Powered by ChatGPT