2022 AMC 10 A
Complete problem set with solutions and individual problem pages
Problem 23 Easy
Isosceles trapezoid has parallel sides and , with and .
There is a point in the plane such that , and . What is ?
- A.
- B.
- C.
- D.
- E.
Answer:B
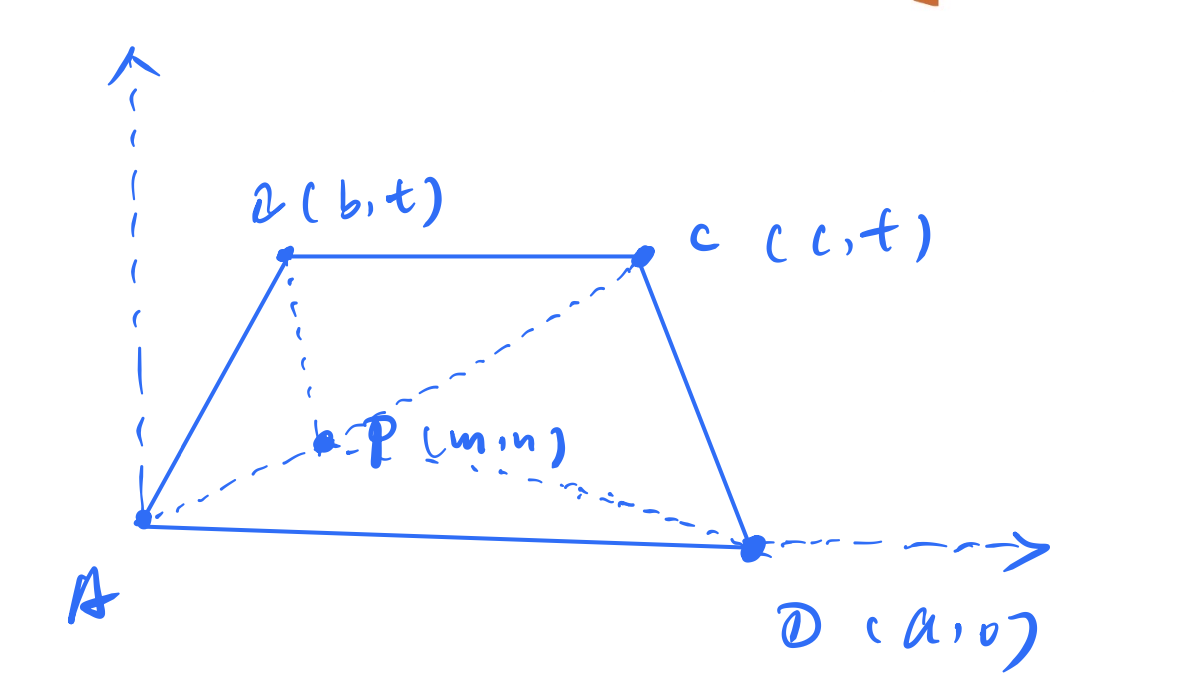
So
Since is equilateral triangle, so .
Thus, .
