AMC 8 Daily Practice - Triangle Properties
Complete problem set with solutions and individual problem pages
Problem 7 Easy
In rectangle , and . The two line segments and divide the area of the rectangle into three equal parts. What is the area of triangle ?
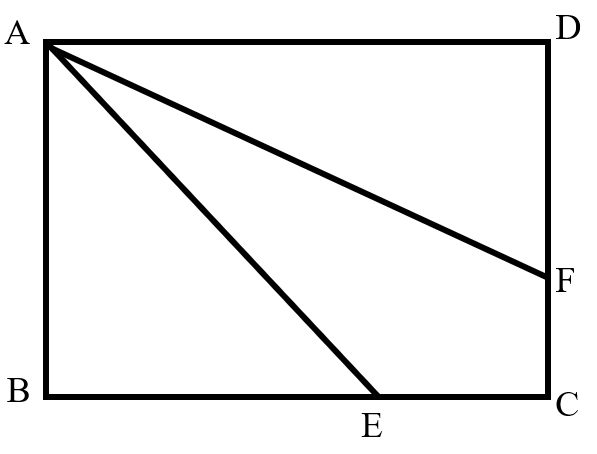
- A.
- B.
- C.
- D.
- E.
Answer:C
The area of rectangle is .
The area of is , so .
The area of is , so .
Connect .
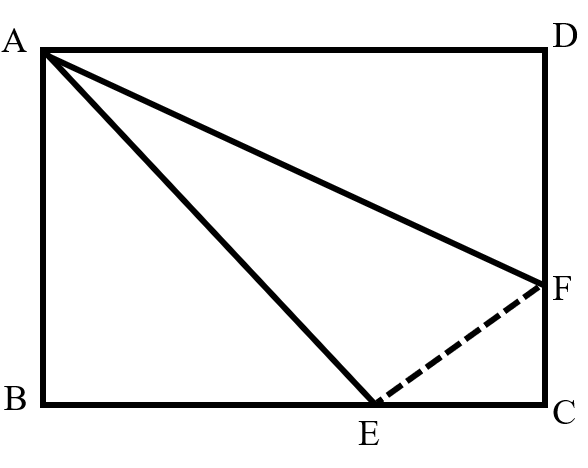
The area of is .
Therefore, the area of is:
Substituting the values and : .
Thus, the area of is .
