2015 AMC 8

Complete problem set with solutions and individual problem pages

Problem 25 Hard

One-inch squares are cut from the corners of this 5 inch square. What is the area in square inches of the largest square that can be fitted into the remaining space?

  • A.

    9

  • B.

    12 \frac 12

  • C.

    15

  • D.

    15 \frac 12

  • E.

    17

Answer:C

We draw a square as shown:

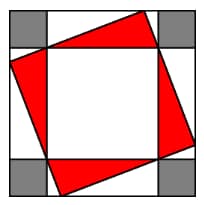
We want to find the area of the biggest square. The area of this square is composed of the center white square and the four red triangles. Because the inner square has an area of (5-2), 3, squared, 9, it also has a length of \sqrt{9}=3. The heights of each of the red triangles are 1 (because the gray squares have lengths of one), and the area of one triangle is namely \frac{3 \cdot 1}{2}. Thus, the combined area of the four triangles is 4 \cdot \frac 32=6. Furthermore, the area of the smaller square is 9. We add these to see that the area of the large square is 9+6=15\implies \boxed{\textbf{(C)}}.

Related Problems
Problem 21 2015 AMC 8
Problem 22 2015 AMC 8
Problem 23 2015 AMC 8
Problem 24 2015 AMC 8
Think Academy Powered by ChatGPT