AMC 8 Daily Practice - Circles

Complete problem set with solutions and individual problem pages

Problem 7 Easy

A rectangle is inscribed with two equal circles, each having an area of 16. A small circle is tangent to three figures (the two large circles and one side of the rectangle). What is the area of the small circle?

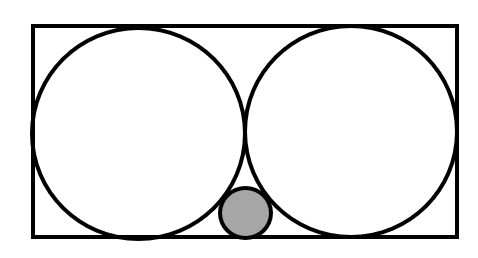
  • A.

    1

  • B.

    1

  • C.

    1

  • D.

    1

  • E.

    1

Answer:E

Let the radius of each large circle be R and the radius of the small circle be r.

Connecting the centers of the three circles forms a triangle.

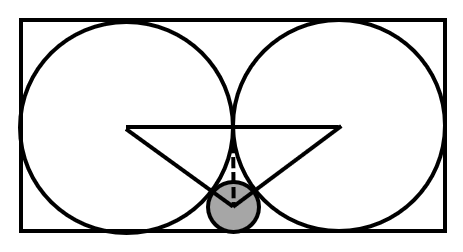
Based on the geometric relationship, we have the equation: R^2 + (R - r)^2 = (R + r)^2

Expanding and simplifying the equation:

R^2 + R^2 - 2Rr + r^2 = R^2 + 2Rr + r^2

2R^2 - 2Rr = R^2 + 2Rr

R^2 = 4Rr

R = 4r

The area of a large circle is given by: S_{\text{large circle}} = \pi R^2 = 16

Substituting R = 4r into the area formula of the large circle:

\pi (4r)^2 = 16, 16\pi r^2 = 16, \pi r^2 = 1

Thus, the area of the small circle is: S_{\text{small circle}} = \pi r^2 = 1.

Related Problems
Problem 4 AMC 8 Daily Practice - Circles
Problem 5 AMC 8 Daily Practice - Circles
Problem 6 AMC 8 Daily Practice - Circles
Problem 8 AMC 8 Daily Practice - Circles
Think Academy Powered by ChatGPT