2017 AMC 8

Complete problem set with solutions and individual problem pages

Problem 16 Hard

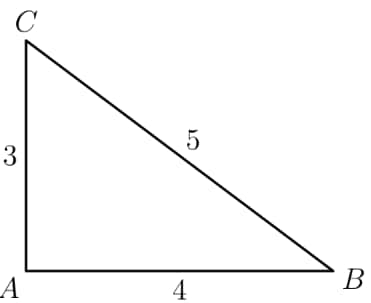
In the figure below, choose point D on \overline{BC} so that \triangle ACD and \triangle ABD have equal perimeters. What is the area of \triangle ABD?

  • A.

    \frac34

  • B.

    \frac32

  • C.

    2

  • D.

    \frac{12}{5}

  • E.

    \frac52

Answer:D

Solution 1

We know that the perimeters of the two small triangles are 3+CD+AD and 4+BD+AD. Setting both equal and using BD+CD = 5, we have BD = 2 and CD = 3. Now, we simply have to find the area of \triangle ABD. Since \frac{BD}{CD} = \frac{2}{3}, we must have \frac{[ABD]}{[ACD]} = 2/3. Combining this with the fact that [ABC] = [ABD] + [ACD] = \frac{3\cdot4}{2} = 6, we get [ABD] = \frac{2}{5}[ABC] = \frac{2}{5} \cdot 6 = \boxed{\textbf{(D) } \frac{12}{5}}.

 

Solution 2

Since \overline{AC} is 1 less than \overline{BC}, \overline{CD} must be 1 more than \overline{BD} to equate the perimeter. Hence, \overline{BD}+\overline{BD}+1=5, so \overline{BD}=2. Therefore, the area of \triangle ABD is \frac{(2)(4)(\sin B)}{2}=4(\frac{3}{5})=\boxed{\textbf{(D) } \frac{12}{5}}

Related Problems
Problem 14 2017 AMC 8
Problem 15 2017 AMC 8
Problem 17 2017 AMC 8
Problem 18 2017 AMC 8
Think Academy Powered by ChatGPT