2014 AMC 8

Complete problem set with solutions and individual problem pages

Problem 14 Medium

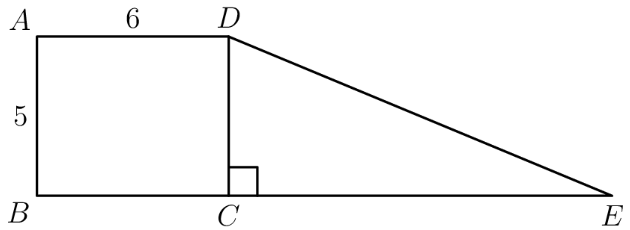
Rectangle ABCD and right triangle DCE have the same area. They are joined to form a trapezoid, as shown. What is DE?

  • A.

    12

  • B.

    13

  • C.

    14

  • D.

    15

  • E.

    16

Answer:B

Solution 1

The area of \bigtriangleup CDE is \frac{DC\cdot CE}{2}. The area of ABCD is AB\cdot AD=5\cdot 6=30, which also must be equal to the area of \bigtriangleup CDE, which, since DC=5, must in turn equal \frac{5\cdot CE}{2}. Through transitivity, then, \frac{5\cdot CE}{2}=30, and CE=12. Then, using the Pythagorean Theorem, you should be able to figure out that \bigtriangleup CDE is a 5-12-13 triangle, so DE=\boxed{13} , or \boxed{(B)}.

 

Solution 2

The area of the rectangle is 5\times6=30. Since the parallel line pairs are identical, DC=5. Let CE be x. \dfrac{5x}{2}=30 is the area of the right triangle. Solving for x, we get x=12. According to the Pythagorean Theorem, we have a 5-12-13 triangle. So, the hypotenuse DE has to be \boxed{(B)}.

Related Problems
Problem 12 2014 AMC 8
Problem 13 2014 AMC 8
Problem 15 2014 AMC 8
Problem 16 2014 AMC 8
Think Academy Powered by ChatGPT