2015 AMC 8
Complete problem set with solutions and individual problem pages
An arithmetic sequence is a sequence in which each term after the first is obtained by adding a constant to the previous term. For example, is an arithmetic sequence with five terms, in which the first term is and the constant added is . Each row and each column in this array is an arithmetic sequence with five terms. The square in the center is labelled as shown. What is the value of ?
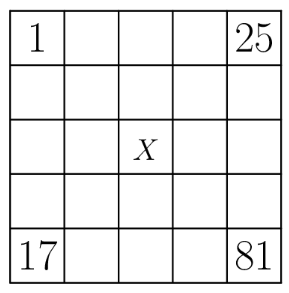
- A.
- B.
- C.
- D.
- E.
Solution 1
We begin filling in the table. The top row has a first term and a fifth term , so we have the common difference is . This means we can fill in the first row of the table:
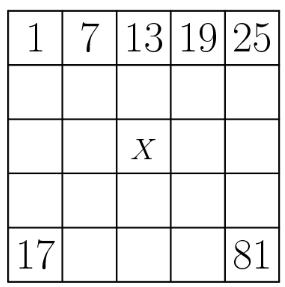
The fifth row has a first term of and a fifth term of , so the common difference is . We can fill in the fifth row of the table as shown:
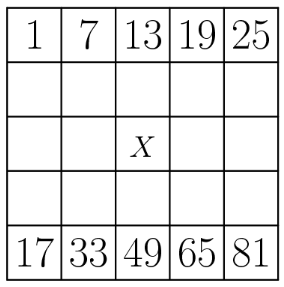
We must find the third term of the arithmetic sequence with a first term of and a fifth term of . The common difference of this sequence is , so the third term is .
Solution 2
The middle term of the first row is , since the middle number is just the average in an arithmetic sequence. Similarly, the middle of the bottom row is . Applying this again for the middle column, the answer is .
