2025 AMC 8
Complete problem set with solutions and individual problem pages
Makayla finds all the possible ways to draw a path in a diamond-shaped grid. Each path starts at the bottom of the grid and ends at the top, always moving one unit northeast or northwest. She computes the area of the region between each path and the right side of the grid. Two examples are shown in the figures below. What is the sum of the areas determined by all possible paths?
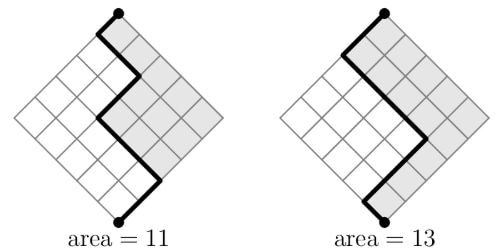
- A.
- B.
- C.
- D.
- E.
Solution 1
Step 1: To find the total number of paths, observe that all paths will have total steps. We have to choose which of these steps will be NE (the rest will be NW). So the total number of paths is . The formula for combinations is: and .
Step 2: Each path splits the total area of in two parts. So, for any path that gives area = , you can find a unique "sister" path that has an area = (in other words, the pair of paths have a combined area of 25). Possible ways to define the "sister" path are:
- Rotate the entire grid

- Swap each step of the original paths (for example, each NW becomes NE) (this is a reflection over the diagonal)
Step 3: There are a few ways to get from this observation to the total area:
- There are pairs of such paths, and the total area of each pair is . So the total area given by all paths is .
- Each of the paths gives an area of if you also count the "sister" paths. Since each "sister" path is also one of the , you have to divide by to avoid double counting. So the total area given by all paths is .
- Note that the average area of two "sister" paths is , so you can think about every path having this area on average. So the total area given by all paths is . The final answer is
Solution 2
If we test this problem on a smaller diamond, we have ways to go from to , and the total area is , so the average area is , which is also the area of the diamond divided by 2. If we assume this is true for a diamond, then the average area is . The number of paths from to is , and .
