2020 AMC 8
Complete problem set with solutions and individual problem pages
Rectangle is inscribed in a semicircle with diameter as shown in the figure. Let and let What is the area of .
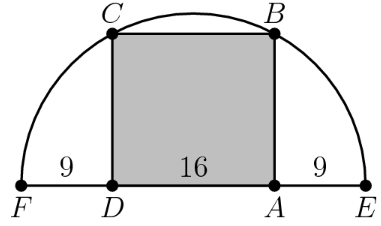
- A.
- B.
- C.
- D.
- E.
Solution 1
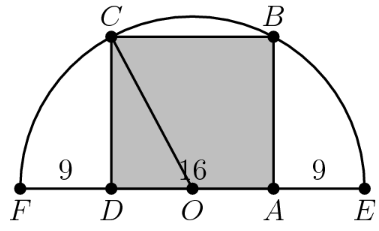
Let be the center of the semicircle. The diameter of the semicircle is , so . By symmetry, is the midpoint of , so . By the Pythagorean theorem in right-angled triangle (or ), we have that (or ) is . Accordingly, the area of is .
Solution 2
Let the midpoint of segment be the origin. Evidently, point and . Since points and share -coordinates with and respectively, it suffices to find the -coordinate of (which will be the height of the rectangle) and multiply this by (which we know is ). The radius of the semicircle is , so the whole circle has equation ; as already stated, has the same -coordinate as , i.e. , so substituting this into the equation shows that . Since at , the y-coordinate of is . Therefore, the answer is .
