2025 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 25 Easy

A point P is chosen at random inside square ABCD. The probability that \overline{AP} is neither the shortest nor the longest side of \triangle{APB} can be written as \frac { a + b \pi - c \sqrt { d } } { e }, where a, b, c, d, and e are positive integers, g c d ( a , b , c , e ) =1 , and d is not divisible by the square of any prime. What is a + b + c + d + e?

  • A.

    25

  • B.

    26

  • C.

    27

  • D.

    28

  • E.

    29

Answer:A

 

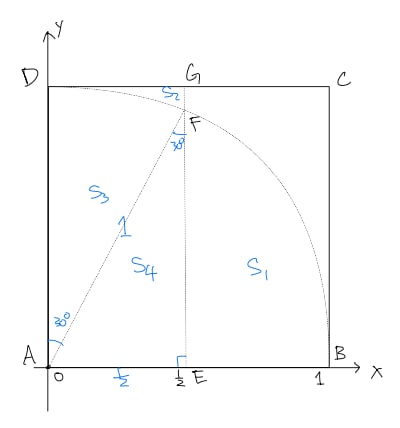
Establish coordinates: A(0,0), B(1,0), C(1,1), D(0,1).

Scenario 1: AB > AP > BP. For point P(x, y):

Condition AP > BP implies x > \frac{1}{2}, and condition AB > AP implies AP < 1.

Point P lies within the unit circle centered at A and to the right of x=\frac{1}{2} which is EF. This defines region S_1.

Scenario 2: AB < AP < BP.

Condition AP < BP implies x < \frac{1}{2}, and condition AB < AP implies AP > 1.

Point P lies outside the unit circle and to the left of x=\frac{1}{2}. This defines region S_2.

Mark S_3 and S_4 as in the diagram too. Notice that \angle OEF = 90^\circ and \frac{OE}{OF}=\frac{1}{2}. So \angle OFE =\angle DAF=30^\circ

Thus S_3=\dfrac{30^\circ}{360^\circ}\pi\cdot1^2=\frac{\pi}{12}, and S_4 =\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{8}.

Also S_2+S_3+S_4=A_{DGEA}=\frac{1}{2}, and S_1+S_3+S_4=\frac{90^\circ}{360^\circ}\pi\cdot1^2=\frac{\pi}{4}.

Final result: S_1 + S_2 = \frac{6 + \pi - 3\sqrt{3}}{12}.

Related Problems
Problem 21 2025 AMC 10 A
Problem 22 2025 AMC 10 A
Problem 23 2025 AMC 10 A
Problem 24 2025 AMC 10 A
Think Academy Powered by ChatGPT