2024 AMC 8
Complete problem set with solutions and individual problem pages
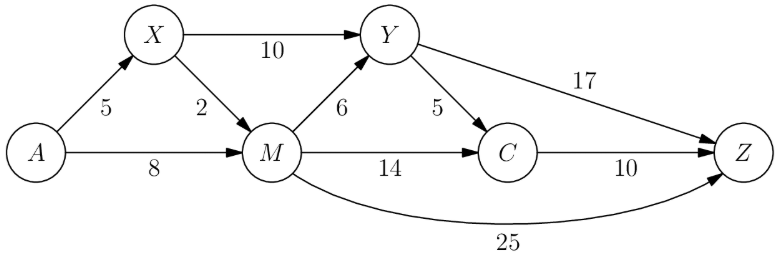
The one-way routes connecting towns and are shown in the figure below(not drawn to scale). The distances in kilometers along each route are marked. Traveling along these routes, what is the shortest distance from A to Z in kilometers?
- A.
- B.
- C.
- D.
- E.
Solution 1
We can simply see that path will give us the smallest value. Adding, . This is nice as it’s also the smallest value, solidifying our answer.
You can also simply brute-force it or sort of think ahead - for example, getting from A to M can be done ways; () or , so you should take the shorter route (). Another example is M to C, two ways - one is and the other is . Take the shorter route. After this, you need to consider a few more times - consider if () is greater than ), which it is not, and consider if ) is greater than () or () which it is not. TLDR: .
Solution 2
We can execute Dijkstra's algorithm by hand to find the shortest path from to every other town, including . This effectively proves that, assuming we execute the algorithm correctly, that we will have found the shortest distance. The distance estimates for each step of the algorithm (from to each node) are shown below:
The steps are as follows: starting with the initial node , set and for all where indicates the distance from to . Consider the outgoing edges and and update the distance estimates and , completing the first row of the table.
The node is the unvisited node with the lowest distance estimate, so we will consider and its outgoing edges and . The distance estimate equals , and the distance estimate updates to , because . This completes the second row of the table. Repeating this process for each unvisited node (in order of its distance estimate) yields the correct distance once the algorithm is complete.
