2020 AMC 10 A
Complete problem set with solutions and individual problem pages
Quadrilateral satisfies , and . Diagonals and intersect at point , and . What is the area of quadrilateral ?
- A.
- B.
- C.
- D.
- E.
Solution 1:
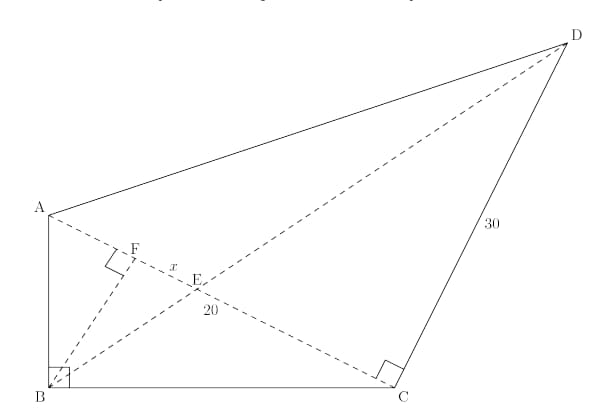
It's crucial to draw a good diagram for this one. Since and , we get . Now we need to find to get the area of the whole quadrilateral. Drop an altitude from to and call the point of intersection . Let . Since , then . By dropping this altitude, we can also see two similar triangles, and . Since is , and , we get that . Now, if we redraw another diagram just of , we get that . Now expanding, simplifying, and dividing by the GCF, we get . This factors to . Since lengths cannot be negative, . Since . So
Solution 2 (Pro Guessing Strats): We know that the big triangle has area 300 . Use the answer choices which would mean that the area of the little triangle is a multiple of 10 . Thus the product of the legs is a multiple of 20 . Guess that the legs are equal to and , and because the hypotenuse is 20 we get . Testing small numbers, we get that when and is indeed a square. The area of the triangle is thus 60 , so the answer is (D) 360
