2015 AMC 8

Complete problem set with solutions and individual problem pages

Problem 12 Medium

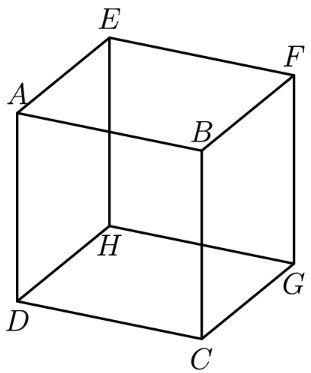
How many pairs of parallel edges, such as \overline{AB} and \overline{GH} or \overline{EH} and \overline{FG}, does a cube have?

  • A.

    6

  • B.

    12

  • C.

    18

  • D.

    24

  • E.

    36

Answer:C

Solution 1

We first count the number of pairs of parallel lines that are in the same direction as \overline{AB}. The pairs of parallel lines are \overline{AB}\text{ and }\overline{EF}, \overline{CD}\text{ and }\overline{GH}, \overline{AB}\text{ and }\overline{CD}, \overline{EF}\text{ and }\overline{GH}, \overline{AB}\text{ and }\overline{GH}, and \overline{CD}\text{ and }\overline{EF}. These are 6 pairs total. We can do the same for the lines in the same direction as \overline{AE} and \overline{AD}. This means there are 6\cdot 3=\boxed{\textbf{(C) } 18} total pairs of parallel lines.

 

Solution 2

Look at any edge, let's say \overline{AB}. There are three ways we can pair \overline{AB} with another edge. \overline{AB}\text{ and }\overline{EF}, \overline{AB}\text{ and }\overline{HG}, and \overline{AB}\text{ and }\overline{DC}. There are 12 edges on a cube. 3 times 12 is 36. We have to divide by 2 because every pair is counted twice, so \frac{36}{2} is \boxed{\textbf{(C) } 18} total pairs of parallel lines.

Related Problems
Problem 10 2015 AMC 8
Problem 11 2015 AMC 8
Problem 13 2015 AMC 8
Problem 14 2015 AMC 8
Think Academy Powered by ChatGPT