2015 AMC 8

Complete problem set with solutions and individual problem pages

Problem 21 Hard

In the given figure, hexagon ABCDEF is equiangular, ABJI and FEHG are squares with areas 18 and 32 respectively, \triangle JBK is equilateral and FE=BC. What is the area of \triangle KBC?

  • A.

    6 \sqrt2

  • B.

    9

  • C.

    12

  • D.

    9 \sqrt2

  • E.

    32

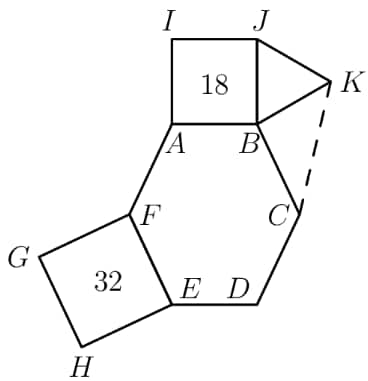
Answer:C

Solution 1

Clearly, since \overline{FE} is a side of a square with area 32, \overline{FE} = \sqrt{32} = 4 \sqrt{2}. Now, since \overline{FE} = \overline{BC}, we have \overline{BC} = 4 \sqrt{2}.

We know that \overline{JB} is a side of a square with area 18, so \overline{JB} = \sqrt{18} = 3 \sqrt{2}. Since \triangle JBK is equilateral, \overline{BK} = \overline{JB} = 3 \sqrt{2}.

Lastly, \triangle KBC is a right triangle. We see that \angle JBA + \angle ABC + \angle CBK + \angle KBJ = 360^{\circ} \rightarrow 90^{\circ} + 120^{\circ} + \angle CBK + 60^{\circ} = 360^{\circ} \rightarrow \angle CBK = 90^{\circ}, so \triangle KBC is a right triangle with legs 3 \sqrt{2} and 4 \sqrt{2}. Now, its area is \dfrac{3 \sqrt{2} \cdot 4 \sqrt{2}}{2} = \dfrac{24}{2} = \boxed{\textbf{(C)}~12}.

 

Solution 2

Since \overline{FE} = \sqrt{32}, and \overline{FE} = \overline{BC}, \overline{BC} = 4\sqrt{2}. Meanwhile, \overline{JB} = 3\sqrt{2}, and since \triangle JBK is equilateral, \overline{BK} = 3\sqrt{2}. If ABCDEF is equiangular, \angle ABC = \frac{180 \cdot (n-2)}{n} = 120^{\circ}, where n is the number of sides of the shape. Adding all the angles around B gives 270^{\circ}, so \angle KBC = 360 - 90 = 270^{\circ}. Because \triangle KBC is right, the area of \triangle KBC = \frac{4\sqrt{2} \cdot 3\sqrt{2}} {2} = 12. Therefore, the answer is \boxed{\textbf{(C)}~12}.

Related Problems
Problem 19 2015 AMC 8
Problem 20 2015 AMC 8
Problem 22 2015 AMC 8
Problem 23 2015 AMC 8
Think Academy Powered by ChatGPT