2017 AMC 8

Complete problem set with solutions and individual problem pages

Problem 22 Hard

In the right triangle ABC, AC=12, BC=5, and angle C is a right angle. A semicircle is inscribed in the triangle as shown. What is the radius of the semicircle?

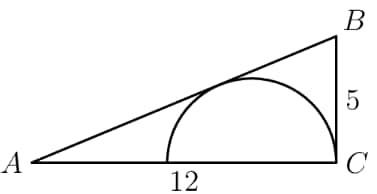
  • A.

    \frac76

  • B.

    \frac{13}{5}

  • C.

    \frac{59}{18}

  • D.

    \frac{10}{3}

  • E.

    \frac{60}{13}

Answer:D

Solution 1 

We can draw another radius from the center to the point of tangency. This angle, \angle{ODB}, is 90^\circ. Label the center O, the point of tangency D, and the radius r.

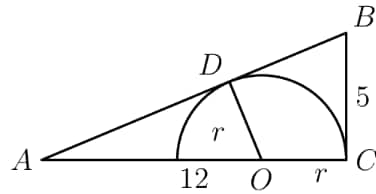
Since ODBC is a kite, then DB=CB=5. Also, AD=13-5=8. By the Pythagorean Theorem, r^2 + 8^2=(12-r)^2. Solving, r^2+64=144-24r+r^2 \Rightarrow 24r=80 \Rightarrow \boxed{\textbf{(D) }\frac{10}{3}}.

 

Solution 2 

If we reflect triangle ABC over line AC, we will get isosceles triangle ABD. By the Pythagorean Theorem, we are capable of finding out that the AB = AD = 13. Hence, \tan \frac{\angle BAD}{2} = \tan \angle BAC = \frac{5}{12}. Therefore, as of triangle ABD, the radius of its inscribed circle r = \frac{\tan \frac{\angle BAD}{2}\cdot (AB + AD - BD)}{2} = \frac{\frac{5}{12} \cdot 16}{2} = \boxed{\textbf{(D) }\frac{10}{3}}

Related Problems
Problem 20 2017 AMC 8
Problem 21 2017 AMC 8
Problem 23 2017 AMC 8
Problem 24 2017 AMC 8
Think Academy Powered by ChatGPT