2024 AMC 8
Complete problem set with solutions and individual problem pages
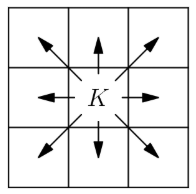
A chess king is said to attack all the squares one step away from it, horizontally, vertically, or diagonally. For instance, a king on the center square of a x grid attacks all other squares, as shown below. Suppose a white king and a black king are placed on different squares of a x grid so that they do not attack each other (in other words, not right next to each other). In how many ways can this be done?
- A.
- B.
- C.
- D.
- E.
Solution 1
If you place a king in any of the corners, the other king will have spots to go and there are corners, so . If you place a king in any of the edges, the other king will have spots to go and there are edges so . That gives us spots for the other king to go into in total. So is the answer.
Solution 2
We see that the center is not a viable spot for either of the kings to be in, as it would attack all nearby squares.
This gives three combinations:
Corner-corner: There are 4 corners, and none of them are touching orthogonally or diagonally, so it's
Corner-edge: For each corner, there are two edges that don't border it,
Edge-edge: The only possible combinations of this that work are top-bottom and left-right edges, so for this type
Multiply by two to account for arrangements of colors to get .
