2017 AMC 8
Complete problem set with solutions and individual problem pages
Mrs. Sanders has three grandchildren, who call her regularly. One calls her every three days, one calls her every four days, and one calls her every five days. All three called her on December , . On how many days during the next year did she not receive a phone call from any of her grandchildren?
- A.
- B.
- C.
- D.
- E.
Solution 1
We use Principle of Inclusion-Exclusion. There are days in the year, and we subtract the days that she gets at least phone call, which is
To this result we add the number of days where she gets at least phone calls in a day because we double subtracted these days, which is
We now subtract the number of days where she gets three phone calls, which is Therefore, our answer is
Solution 2
Note that so there is a cycle every days.
As shown below, all days in a cycle that Mrs. Sanders receives a phone call from any of her grandchildren are colored in red, yellow, or green.
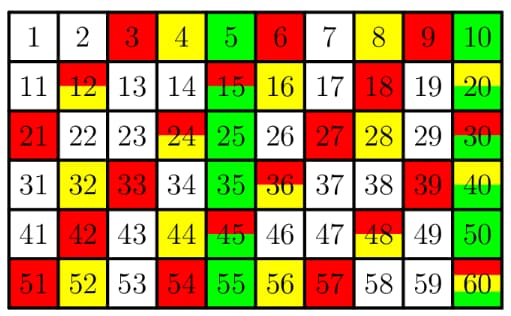
The year has days, or cycles and days.
- For each cycle, there are days that Mrs. Sanders does not receive a phone call, as indicated by the white squares.
- For the last days, there are days that Mrs. Sanders does not receive a phone call, as indicated by the first days in a cycle. Together, the answer is
