2022 AMC 8
Complete problem set with solutions and individual problem pages
Steph scored baskets out of attempts in the first half of a game, and baskets out of attempts in the second half. Candace took attempts in the first half and attempts in the second. In each half, Steph scored a higher percentage of baskets than Candace. Surprisingly they ended with the same overall percentage of baskets scored. How many more baskets did Candace score in the second half than in the first?
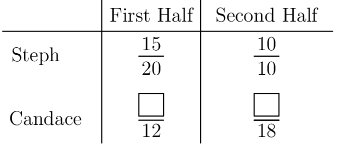
- A.
- B.
- C.
- D.
- E.
Solution 1 (Inequalities)
Let be the number of shots that Candace made in the first half, and let be the number of shots Candace made in the second half. Since Candace and Steph took the same number of attempts, with an equal percentage of baskets scored, we have In addition, we have the following inequalities:
and
Pairing this up with we see the only possible solution is for an answer of
Solution 2 (Answer Choices)
Clearly, Steph made shots in total. Also, due to parity reasons, the difference between the amount of shots Candace made in the first and second half must be odd. Thus, we can just test 7, 9, and 11, and after doing so we find that the answer is
