2025 AMC 10 A
Complete problem set with solutions and individual problem pages
Problem 23 Easy
Triangle has side lengths , , and . The bisector of and the altitude to side intersect at point . What is ?
- A.
- B.
- C.
- D.
- E.
Answer:D
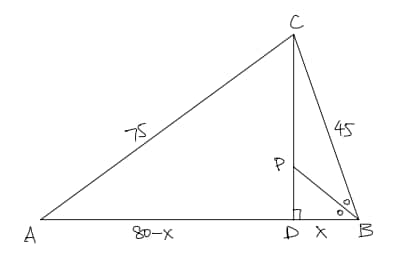
Set , making .
This gives .
Solving: , and , so .
By the angle bisector theorem,
So
Therefore:
Thus .
