2020 AMC 8
Complete problem set with solutions and individual problem pages
A game board consists of squares that alternate in color between black and white. The figure below shows square in the bottom row and square in the top row. A marker is placed at A step consists of moving the marker onto one of the adjoining white squares in the row above. How many -step paths are there from to (The figure shows a sample path.)

- A.
- B.
- C.
- D.
- E.
Solution 1
Notice that, to step onto any particular white square, the marker must have come from one of the or white squares immediately beneath it (since the marker can only move on white squares). This means that the number of ways to move from to that square is the sum of the number of ways to move from to each of the white squares immediately beneath it (also called the Waterfall Method). To solve the problem, we can accordingly construct the following diagram, where each number in a square is calculated as the sum of the numbers on the white squares immediately beneath that square (and thus will represent the number of ways to remove from to that square, as already stated).

The answer is therefore .
Solution 2
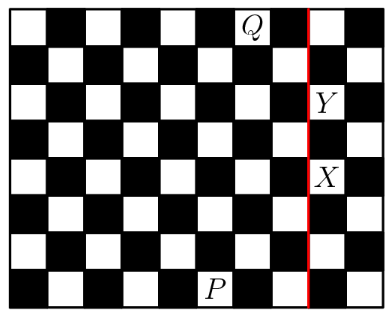
Suppose we "extend" the chessboard infinitely with additional columns to the right, as shown below. The red line shows the right-hand edge of the original board.
The total number of paths from to , including invalid paths which cross over the red line, is then the number of paths which make steps up-and-right and steps up-and-left, which is . We need to subtract the number of invalid paths, i.e. the number of paths that pass through or . To get to , the marker has to make up-and-right steps, after which it can proceed to with steps up-and-left and step up-and-right. Thus, the number of paths from to that pass through is . Similarly, the number of paths that pass through is . However, we have now double-counted the invalid paths which pass through both and ; from the diagram, it is clear that there are only of these (as the marker can get from to by a step up-and-left and a step-up-and-right in either order). Hence the number of invalid paths is , and the number of valid paths from to is .
