AMC 8 Daily Practice - The Rule of Arithmetic Sequences
Complete problem set with solutions and individual problem pages
As shown in the diagram, a regular hexagon (with all sides equal) is positioned on a number line. Points and correspond to numbers and , respectively. When the hexagon is rotated clockwise around a vertex, after rotation, point aligns with the number . Continuing this rotation pattern, identify which vertex of the hexagon corresponds to the number on the number line.
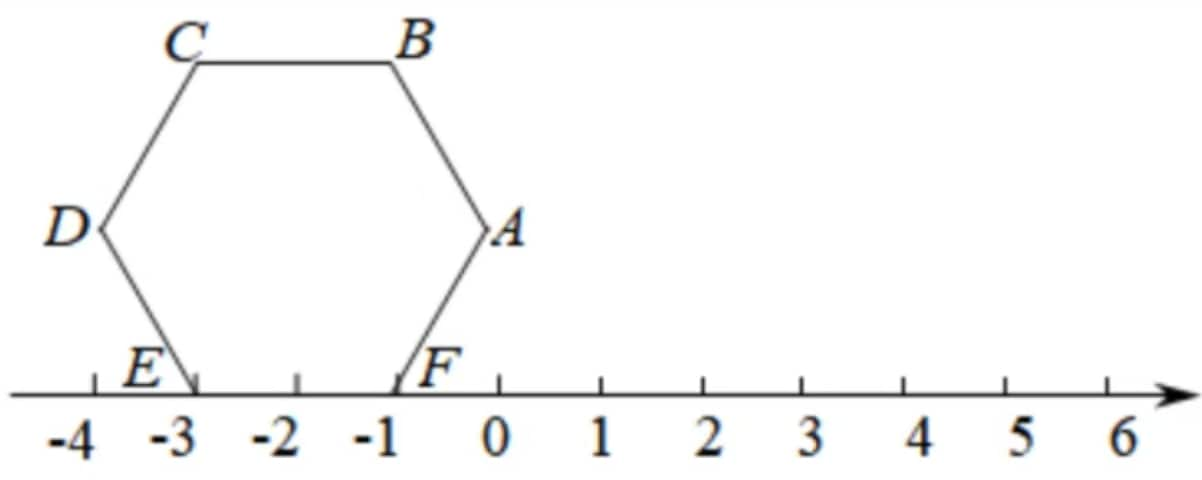
- A.
- B.
- C.
- D.
- E.
From the first rotation, point moves to , indicating the side length of the hexagon is (distance between and ).
Observing the rotation pattern:
- After rotation: Point
- After rotations: Point
- After rotations: Point
- After rotations: Point
- After rotations: Point
- After rotations: Point
- After rotations: Point
This establishes a periodic pattern with period .
The general formula for the position after rotations is:
Set
Determine the position within the -rotation cycle:
A remainder of corresponds to the vertex in the cycle (E).
Final result:
