2014 AMC 8

Complete problem set with solutions and individual problem pages

Problem 25 Hard

A straight one-mile stretch of highway, 40 feet wide, is closed. Robert rides his bike on a path composed of semicircles as shown. If he rides at 5 miles per hour, how many hours will it take to cover the one-mile stretch?

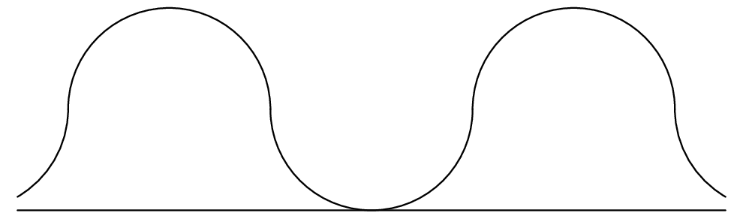
Note: 1 mile = 5280 feet

  • A.

    \frac{\pi}{11}

  • B.

    \frac{\pi}{10}

  • C.

    \frac{\pi}{5}

  • D.

    \frac{2\pi}{5}

  • E.

    \frac{2\pi}{3}

Answer:B

There are two possible interpretations of the problem: that the road as a whole is 40 feet wide, or that each lane is 40 feet wide. Both interpretations will arrive at the same result. However, let us stick with the first interpretation for simplicity. Each lane must then be 20 feet wide, so Robert must be riding his bike in semicircles with radius 20 feet and diameter 40 feet. Since the road is 5280 feet long, over the whole mile, Robert rides \frac{5280}{40} =132 semicircles in total. Were the semicircles full circles, their circumference would be 2\pi\cdot 20=40\pi feet; as it is, the circumference of each is half that, or 20\pi feet. Therefore, over the stretch of highway, Robert rides a total of 132\cdot 20\pi =2640\pi feet, equivalent to \frac{\pi}{2} miles. Robert rides at 5 miles per hour, so divide the \frac{\pi}{2} miles by 5 mph (because t = \frac{d}{r} and time = distance/rate) to arrive at \boxed{\textbf{(B) }\frac{\pi}{10}} hours.

Related Problems
Problem 21 2014 AMC 8
Problem 22 2014 AMC 8
Problem 23 2014 AMC 8
Problem 24 2014 AMC 8
Think Academy Powered by ChatGPT