2023 AMC 8

Complete problem set with solutions and individual problem pages

Problem 16 Hard

The letters \text{P}, \text{Q}, and \text{R} are entered into a 20\times20 table according to the pattern shown below. How many \text{P}s, \text{Q}s, and \text{R}s will appear in the completed table?

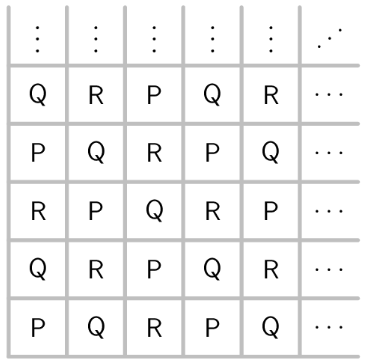
  • A.

    132\text{ Ps, }134\text{ Qs, }134\text{ Rs}

  • B.

    133\text{ Ps, }133\text{ Qs, }134\text{ Rs}

  • C.

    133\text{ Ps, }134\text{ Qs, }133\text{ Rs}

  • D.

    134\text{ Ps, }132\text{ Qs, }134\text{ Rs}

  • E.

    134\text{ Ps, }133\text{ Qs, }133\text{ Rs}

Answer:C

Solution 1

In our 5\times5 grid, there are 8,9 and 8 of the letters \text{P}, \text{Q}, and \text{R}, respectively, and in a 2\times2 grid, there are 1,2 and 1 of the letters \text{P}, \text{Q}, and \text{R}, respectively. We see that in both grids, there are x, x+1, and x of the \text{P}, \text{Q}, and \text{R}, respectively. This is because in any n\times n grid with n\equiv2\pmod3, there are x, x+1, and x of the \text{P}, \text{Q}, and \text{R}, respectively. We can see that the only answer choice which satisfies this condition is \boxed{\textbf{(C)}~133\text{ Ps, }134\text{ Qs, }133\text{ Rs}}.

 

Solution 2

Since 20\equiv2\pmod3 and \text{Q} is in the 2nd diagonal, it is also in the 20th diagonal, and so we find that there are 2(2 + 5 + 8 + 11 + 14 + 17) + 20 = 134 \text{Qs}. Since all the \text{P}'s and \text{R}'s are symmetric, the answer is \boxed{\textbf{(C)}~133\text{ Ps, }134\text{ Qs, }133\text{ Rs}}.

Related Problems
Problem 14 2023 AMC 8
Problem 15 2023 AMC 8
Problem 17 2023 AMC 8
Problem 18 2023 AMC 8
Think Academy Powered by ChatGPT