AMC 10 Daily Practice - Tangency

Complete problem set with solutions and individual problem pages

Problem 3 Easy

Circle C_1 and C_2 each have radius 1, and the distance between their centers is \frac{1}{2}. Circle C_3 is the largest circle internally tangent to both C_1 and C_2. Circle C_4 is internally tangent to both C_1 and C_2 and externally tangent to C_3. What is the radius of C_4? (2023 AMC 10A Problems, Quetsion #22)

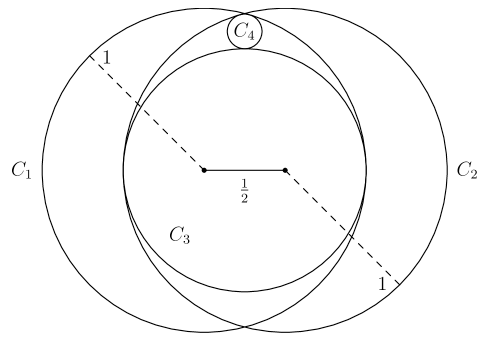
  • A.

    \frac{1}{14}

  • B.

    \frac{1}{12}

  • C.

    \frac{1}{10}

  • D.

    \frac{3}{28}

  • E.

    \frac{1}{9}

Answer:D

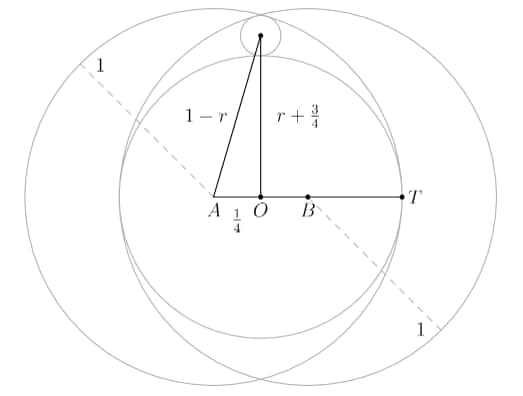
Let O be the center of the midpoint of the line segment connecting both the centers, say A and B.

 

Let the point of tangency with the inscribed circle and the right larger circles be T.

 

Then OT = BO + BT = BO + AT - \frac{1}{2} = \frac{1}{4} + 1 - \frac{1}{2} = \frac{3}{4}.

 

Since C_4 is internally tangent to C_1, center of C_4, C_1 and their tangent point must be on the same line.

 

Now, if we connect centers of C_4, C_3 and C_1/C_2, we get a right angled triangle.

 

Let the radius of C_4 equal r. With the pythagorean theorem on our triangle, we have

 

\left(r+\frac{3}{4}\right)^2+\left(\frac{1}{4}\right)^2=(1-r)^2

 

Solving this equation gives us

 

r = \boxed{\textbf{(D) } \frac{3}{28}}

Related Problems
Problem 1 AMC 10 Daily Practice - Tangency
Problem 2 AMC 10 Daily Practice - Tangency
Think Academy Powered by ChatGPT