2016 AMC 8
Complete problem set with solutions and individual problem pages
A semicircle is inscribed in an isosceles triangle with base and height so that the diameter of the semicircle is contained in the base of the triangle as shown. What is the radius of the semicircle?
- A.
- B.
- C.
- D.
- E.
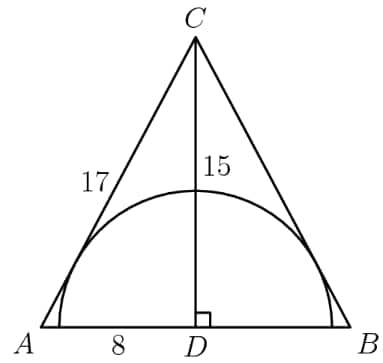
First, we drop a perpendicular, shown above, to the base of the triangle, cutting the triangle into two congruent right triangles. This triangle is isosceles, which means perpendiculars are medians and vice versa. The base of the resulting right triangle is for both sides, and the height is as given. Using the Pythagorean theorem, we can find the length of the hypotenuse, or Using the two legs of the right triangle, we find the area of the right triangle, . times results in the radius, which is the height of the right triangle when using the hypotenuse as the base. Hence, the answer is .
