2022 AMC 10 A
Complete problem set with solutions and individual problem pages
Problem 15 Easy
Quadrilateral with side lengths , , , is inscribed in a circle. The area interior to the circle but exterior to the quadrilateral can be written in the form , where , , and are positive integers such that and have no common prime factor. What is ?
- A.
- B.
- C.
- D.
- E.
Answer:D
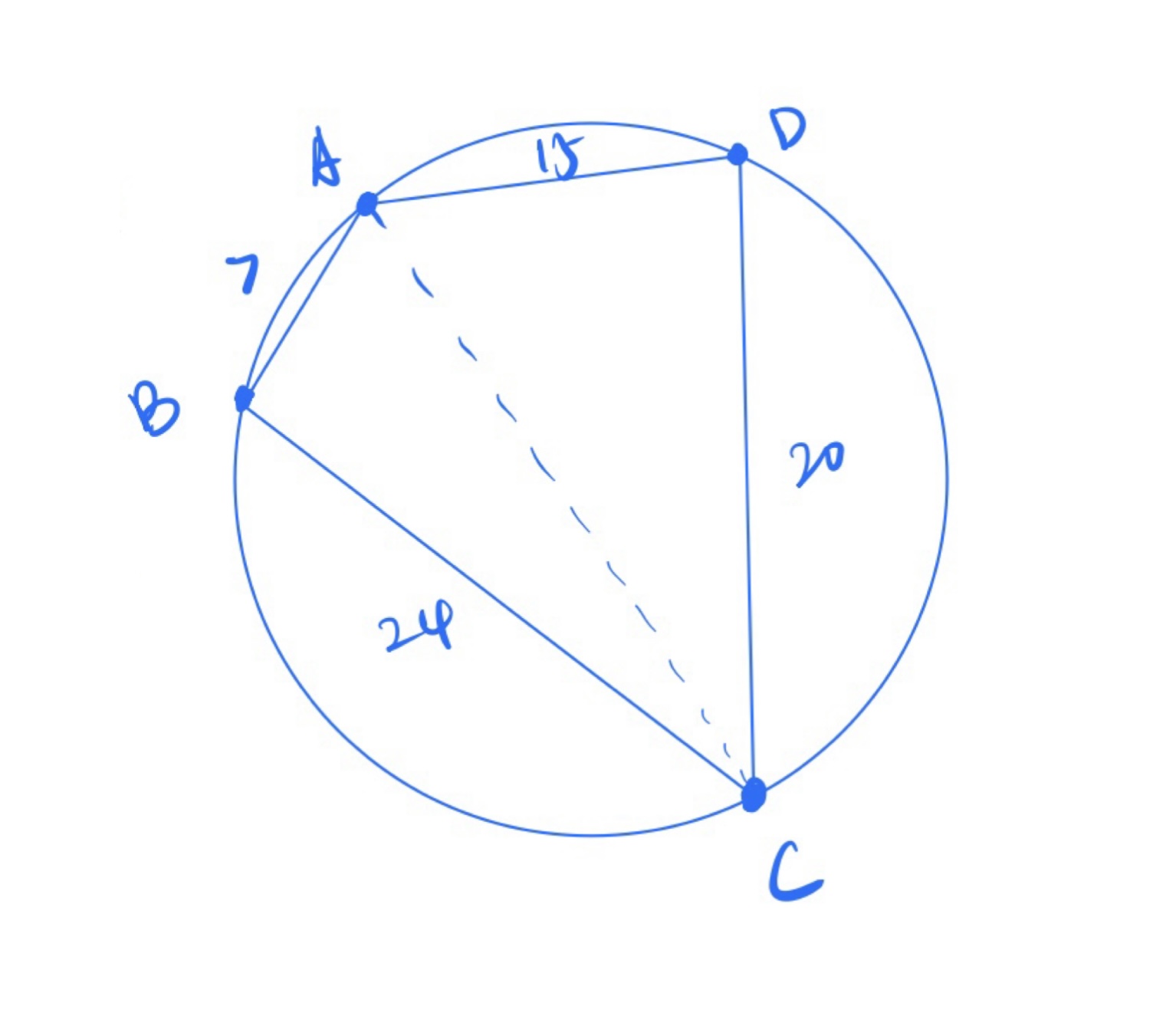
If
, so there is a contradiction.
If , we also have a contradiction.
,
AC is the diameter of the circle.
,
.
.
